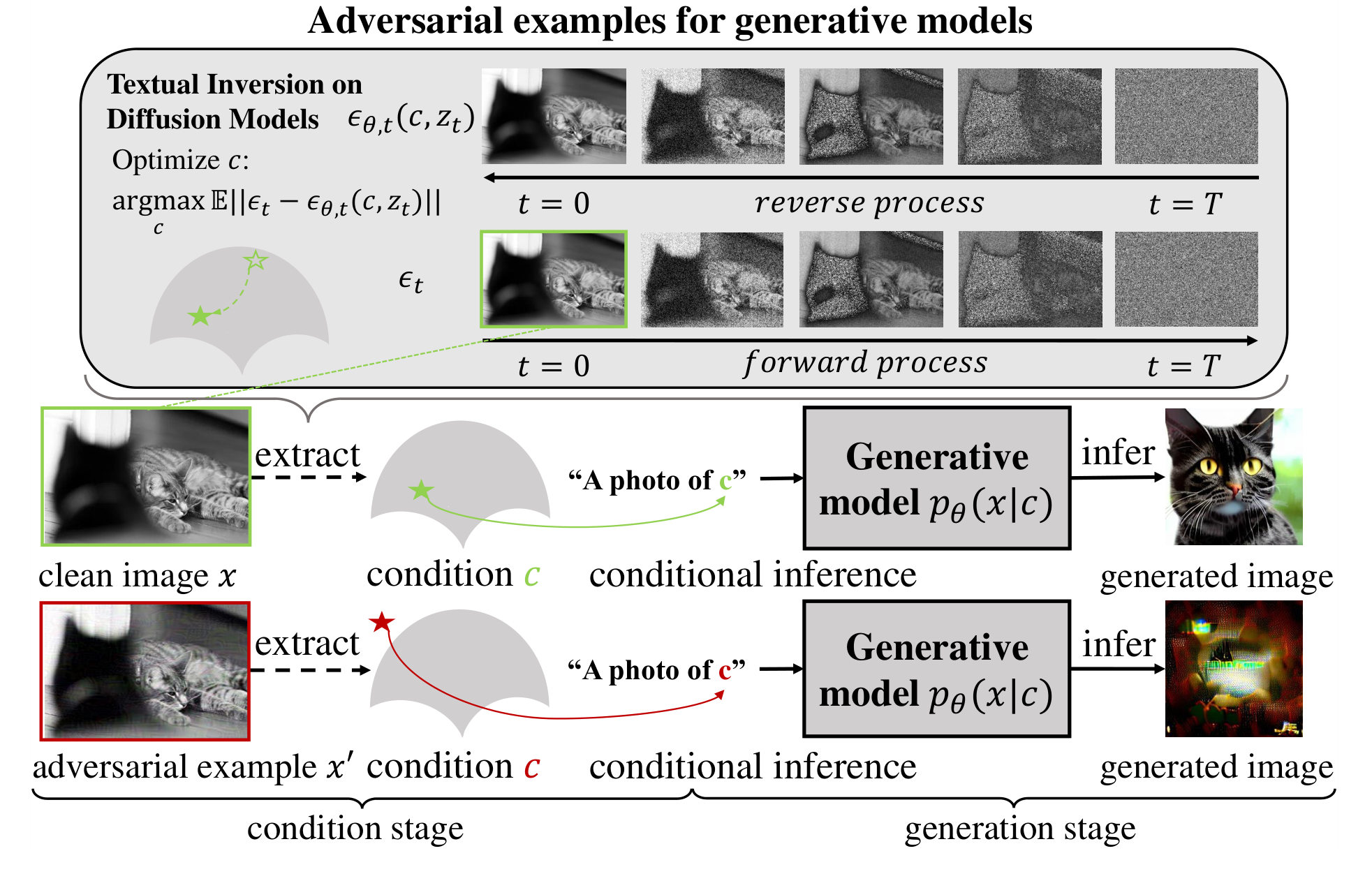
モンテカルロ法を用いて生成過程の潜在変数をおかしくするAEsを生成する手法を提案。PhotoGuardは実写画像がターゲットだったが、AdvDMはアートがターゲット。
課題
- AEsで拡散モデルを攻撃しようにも、分類モデルと比べて難しい
- 最適化のフローが変分境界を通して間接的に行われる=AEsが直接適用不可能
- 拡散モデルに対するAEsの既存の方法がない
AdvDM

特徴抽出をOODにするノイズが生成されるように学習。その損失関数にモンテカルロ法を使う。
前提
実分布を $ q(x) $ 生成分布を $ p(x) $ すると摂動 $ \delta $ は次式で求められる。
しかし、 $ q(x) $ は未知なので、モンテカルロ法を使って近似する。$ p_\theta (x) $を使って、$ p_\theta (x+\delta) $を近似する。
各時点の実分布の事後分布 $ q\left(x_{1: T}^{\prime} \mid x_0^{\prime}\right) $は画像 $ x_0 $と独立な固定パラメータのガウス分布なので、生成分布 $ p_\theta (x\prime_(0:T)) $ は$ q\left(x_{1: T}^{\prime} \mid x_0^{\prime}\right) $で正則化できる。
最適化
$E_{x_{1: T} \sim u\left(x_{1: T}\right)} \mathcal{L}_{D M}(\theta)$は期待値の損失なので、普通のAEsと違い勾配がわからない。そこで、モンテカルロ法を使って勾配を推定する。
敵対的な生成分布 $ u (x\prime_(1:T)) $ から $ x\prime_(1:T) $ をサンプリングして、$ L_{D M}(\theta) $ の勾配を推定する。
この推定された勾配を使ってFGSMを行う。
異なる潜在変数になる各サンプルをイテレーション。
評価
=コピーライトの心配なし
特徴抽出された特徴がOODになっていることを評価
画像から実際に抽出される条件 $c_g$のほうが無条件でサンプリングされる $c$よりも画像との類似性が高いはず

CFGっぽい
アートトレースが危惧されるシナリオ
- Text InversionベースのT2I
- Text Inversionベースのスタイル変換
- I2Iの変換
結果

スタイルを強く転送しようとすると、崩壊している感じがする。